用C++ AMP写一个GPU压力测试程序
前言
我们今天尝试写一个GPU压力测试程序,如果我们写一个CPU压力测试程序,我们知道我们需要让CPU进行繁重的计算,那么对于GPU压力测试程序该怎么做呢?
C++ AMP
首先我们应该会想到,该如何让我们的代码运行在GPU上?一些图形库API会进行硬件加速,如Direct3D和OpenGL。一些异构编程框架如CUDA与OpenCL可以指定代码在GPU上运行。然而这些库使用起来并不简单, 我们可能需要很长时间的学习。那么有没有一种简单并且方便编程的库呢?微软给我们提供了一个选择:C++ AMP(Accelerated Massive Parallelism)库。C++ AMP是一个异构编程框架,使用者可以很方便的利用GPU进行并行计算。C++ AMP库类似于C++ STL库,在Visual Studio中我们只要包含相应的头文件就可以使用它。关于C++ AMP库的详细使用方法,请参考MSDN链接:https://msdn.microsoft.com/zh-cn/library/hh265136。
需要注意的是使用C++ AMP库有如下限制:
- 只能在Windows平台下使用Visual Studio进行编程
- Windows最低版本Windows 7
- Visual Studio最低版本Visual Studio 2012
- 只能运行在最低支持DirectX11的显卡上(独立显卡或核心显卡)
曼德勃罗特集
解决了使用C++ AMP在GPU上进行计算的问题?现在我们该思考让GPU计算什么的问题。我们的目标是实现一个GPU压力测试程序,所以我们得保证我们的计算足够复杂。我们知道GPU有大量的计算核心,所以我们可能需要进行并行计算,这样才能让GPU产生压力。曼德勃罗特集是易并行计算的一个典型例子,并且该集合以图像的方式呈现后很有意思,该集合在有些位置可以进行无限放大,如下图:

曼德勃罗特(Mandelbrot)集是一种复平面上的点集。对任意复数C,我们有如下公式:
\begin{align} &Z_{n+1} = (Z_n)^2 + C \\ &n >= 0 \\ &Z_0 = 0 \end{align}
所有使得无限迭代后的结果能保持有限数值的C的集合,就构成曼德勃罗特集。在计算机中对于无限迭代我们只能取一个固定的值例如256,意思就是最大计算到$Z_{256}$,有限数值指的是复数$Z_n$的模小于某个指定的值例如2,对于不同的C有的C可能迭代几次后$Z_n$模就大于2,有的C可能迭代256次后$Z_n$的模还在范围内。我们可以记录下不同的C的迭代值。例如我们可以计算(-2, 2),(2, 2),(2, -2),(-2, -2)这4个点范围内等比例划分的500*500的不同的C的迭代值,将迭代值[0~256]映射到颜色空间上,将C对应到图片的像素点位置,我们就可以得到500*500的绚丽图片,如同上图所示。
如下为使用C++ AMP计算曼德勃罗特集的核心算法:
/// <SUMMARY>
/// 曼德勃罗特图像结构
/// </SUMMARY>
struct MandelbrotImage
{
unsigned int Width; // 图像宽
unsigned int Height; // 图像高
unsigned int* PData; // 存储图像数据
};
/// <SUMMARY>
/// 曼德勃罗特参数结构
/// </SUMMARY>
LTEMPLATE struct MandelbrotParam
{
Type RealMin; // 实部最小值
Type ImgMin; // 虚部最小值
Type RealMax; // 实部最大值
Type ImgMax; // 虚部最大值
unsigned int MaxIter; // 最大迭代次数
};
template<typename Type> bool AMPGenerateMandelbrot(const MandelbrotParam<Type>& param, IMandelbrotImage& image)
{
const Type REAL_MIN = param.RealMin;
const Type REAL_MAX = param.RealMax;
const Type IMG_MIN = param.ImgMin;
const Type IMG_MAX = param.ImgMax;
const unsigned int HEIGHT = image.Height;
const unsigned int WIDTH = image.Width;
const unsigned int MAX_ITER = param.MaxIter;
// 实部递进比例
const Type SCALE_REAL = (REAL_MAX - REAL_MIN) / WIDTH;
// 虚部递进比例
const Type SCALE_IMG = (IMG_MAX - IMG_MIN) / HEIGHT;
// 定义图像在显存中的映射
array_view<unsigned int, 2> imageView(HEIGHT, WIDTH, image.PData);
// 放弃内存到显存的复制
imageView.discard_data();
// 使用GPU进行并行运算
parallel_for_each(imageView.extent, [=](index<2> i) restrict(amp)
{
int iReal = i[1]; // 列索引, 也就是X轴(实轴)
int iImg = i[0]; // 行索引, 也就是Y轴(虚轴)
/*
曼德勃罗特集迭代公式Zn+1=(Zn)^2+C
*/
// 每个点对应的C
Type cReal = REAL_MIN + (Type)iReal * SCALE_REAL;
Type cImg = IMG_MIN + (Type)(HEIGHT - iImg) * SCALE_IMG;
// Zn初始为0 0
Type zReal = 0;
Type zImg = 0;
const Type MAX_LENGTH = 4.0;
Type length = 0;
Type temp = 0;
unsigned int count = 0;
do
{
count++;
// 计算Zn+1的实部
temp = zReal * zReal - zImg * zImg + cReal;
// 计算Zn+1的虚部
zImg = 2 * zReal * zImg + cImg;
zReal = temp;
length = zReal * zReal + zImg * zImg;
} while ((count < MAX_ITER) && (length < MAX_LENGTH));
// 计算色相
float n = count / 64.0f;
float h = 1.0f - 2.0f * fabs(0.5f - n + floor(n));
// 逃逸点的亮度为0, 逃逸点即是cout == MAX_ITER
float bfactor = direct3d::clamp((float)(MAX_ITER - count), 0.0f, 1.0f);
imageView[i] = HSB2RGB(h, 0.75f, (1.0f - h * h * 0.83f) * bfactor);
});
// 将显存中的数据拷贝回内存
imageView.synchronize();
return true;
}
GPU压力测试程序
现在我们解决了计算的问题,我们该考虑如何让程序持续不断的计算曼德勃罗特集,我们可以考虑选取一些特殊的中心点,让程序以中心点来计算曼德勃罗特集。例如选取(0, 0)为中心点,我们第一次可以在矩形(-2, 2),(2, 2),(2, -2),(-2, -2)范围内等比例取500*500个点进行计算,第二次我们在矩形(-1.9, 1.9),(1.9, 1.9),(1.9, -1.9),(-1.9, -1.9)范围内等比例取500*500个点进行计算,这样持续下去就会有放大图像的效果,如上面动图展示。
理论上我们可以对曼德勃罗特集的细节进行无限放大,但是计算机的浮点数有精度值,例如在单精度的情况下当我们放大到矩形(-0.00001, 0.00001),(0.00001, 0.00001),(0.00001, -0.00001),(-0.00001, -0.00001)时,后续的计算可能就不是很准确了。所以当我们放大到极限尺寸时,可以再做缩小的动作。如下图所示:
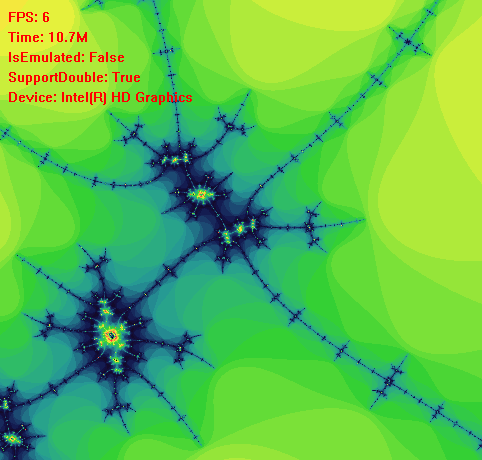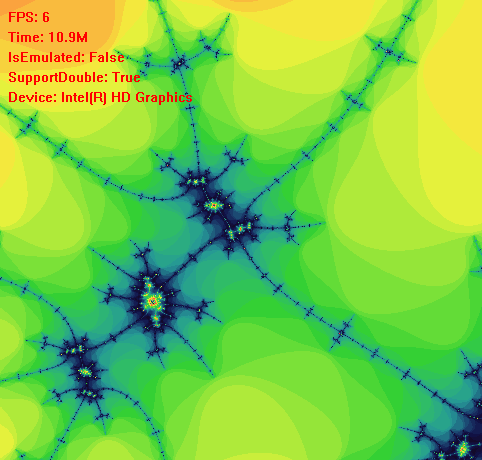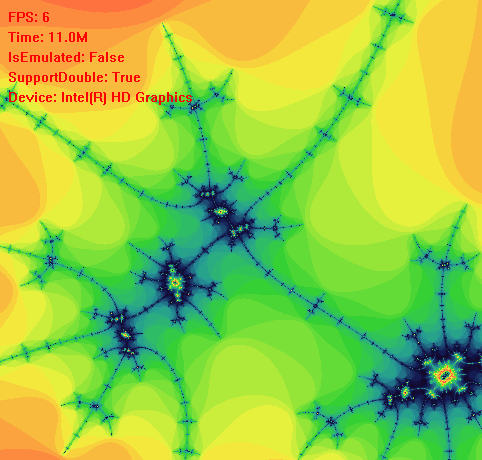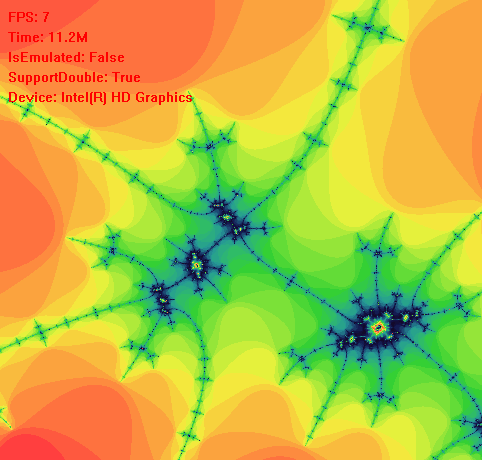
实际上我们还可以多设置几个中心点,一个中心点计算完成后,再计算另一个中心点,循环往复。
程序源码可在如下链接查看:https://github.com/BurnellLiu/BLHWScaner/tree/master/GPUStress
编译好的程序执行档可在如下链接获取:https://github.com/BurnellLiu/BLHWScaner/tree/master/Bin/GPUStress
程序的界面上可以看到当前的FPS即每秒钟计算和绘制的帧数,可以通过它简单观察GPU的性能。
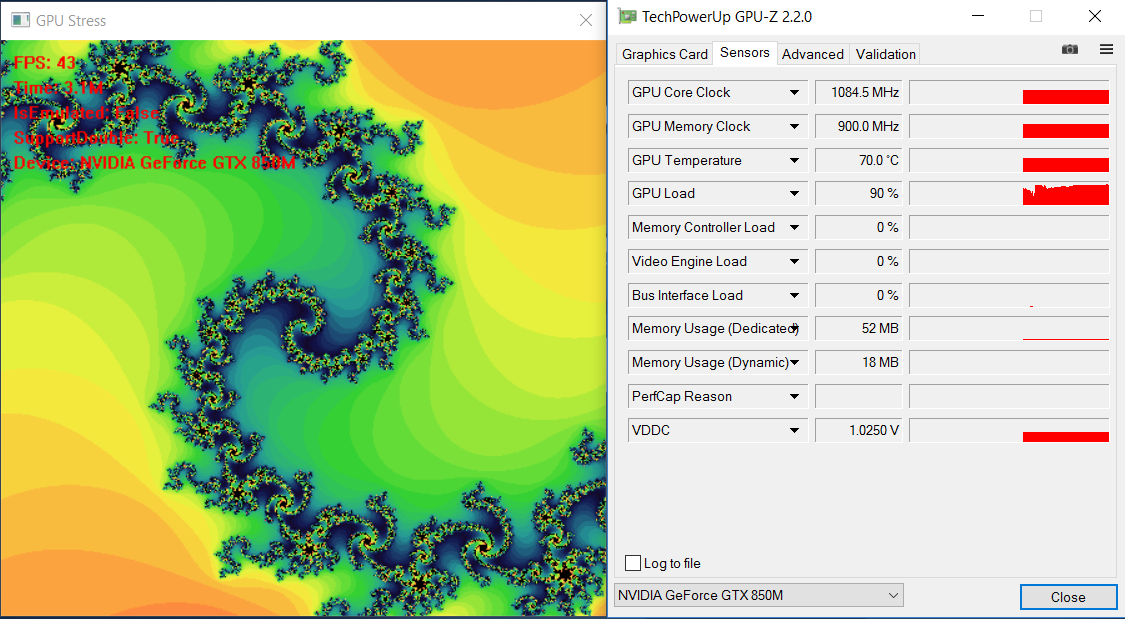
通过GPU-Z工具可以看到我们程序在运行时GPU的负载,如下是程序运行1分钟后的情况,我们可以看到GPU温度为66摄氏度,GPU负载为88%:
程序运行3分钟后的情况如下:
我们可以看到GPU温度上升到70摄氏度,GPU负载为90%








还没有人评论...