P问题 NP问题 NPC问题 NP-Hard问题

概念
P问题(Polynomial Problem):可以在多项式时间内解决的问题。
NP问题(Non-Deterministic Polynomial Problem):可以在多项式时间内验证一个解的问题。
NPC问题(NP Complete Problem):所有NP问题都可以在多项式时间内约化(Reducibility)到它并且它本身就是一个NP问题的问题。
NP-Hard问题(NP Hard Problem):所有NP问题都可以在多项式时间内约化(Reducibility)到它的问题。
它们的关系如下:
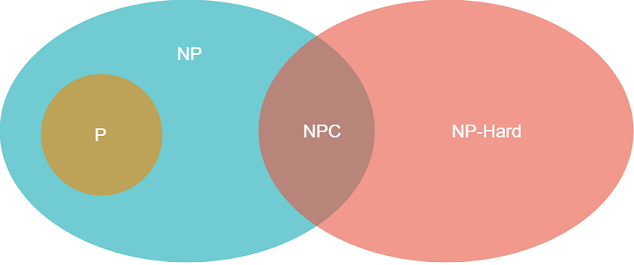
多项式时间:我们知道时间复杂度有O(1),O(n),O(logn),O(n^a),O(a^n),O(n!)等,我们把O(1),O(n),O(logn),O(n^a)等称为多项式级的复杂度,我们把O(a^n),O(n!)称为非多项式级的复杂度。非多项式级的复杂度在数据量变大后,需要的时间太多。
约化:问题A约化为问题B的含义就是,可以用问题B的解法解决A。例如我们有问题A:求解一元一次方程bx+c=0,问题B:求解二元一次方程ax^2+bx+c=0。如果我们知道问题B的解法,那么一定可以知道问题A的解法,因为只要我们令a=0,问题B就和问题A等价,所以我们可以说“问题A可约化为问题B”。很显然当我们说“问题A可约化为问题B”,那么问题B的时间复杂度一定高于或者等于问题A的时间复杂度。其次约化还具有一个重要性质:约化具有传递性。也就是说如果问题A可约化为问题B,问题B可约化为问题C,那么问题A一定可约化为问题C。
P问题
排序问题就是一个P问题,因为我们有时间复杂度为O(n^2)的冒泡排序算法。
NP问题
很多问题很难找到多项式时间的解法(不一定存在),但我们可以在多项式时间内判断一个解是否正确。如下图(图片来源于维基百科)的哈密顿回路问题,目前没有多项式时间的算法找到哈密顿回路,但我们很容易判断一个回路是否是哈密顿回路(看是不是所有顶点都在回路中,并且路径不重复)。
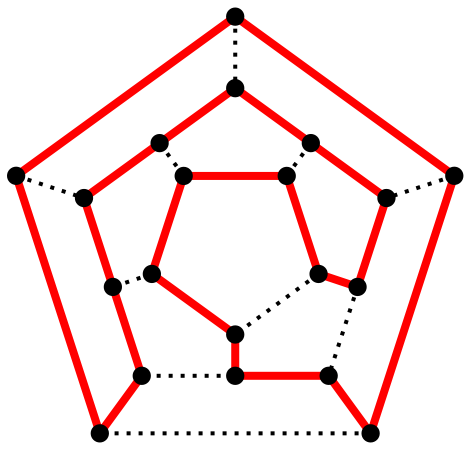
很显然P问题是NP问题的子集,因为P问题有正解,所以验证任意解只需要比较就可以。
NPC问题
我们知道一个问题约化后,时间复杂度可能增加了,问题的应用范围也可能增大了。那么通过不断的约化,我们能否找到一个超级NP问题,使得所有的NP问题都可以约化到它?答案是肯定的,这就是NPC问题。可以想象如果我们解决了NPC问题,那么所有的NP问题都将被解决,这种问题的存在真的让人惊叹。此外NPC问题事实上不只一个,它有很多个,这是一类问题。很显然NPC问题是可以相互约化的,也就是说如果我们想证明一个问题是NPC问题,只要证明这个问题是NP问题并且已知的一个NPC问题可以约化到它。那么第一个NPC问题是怎么来的?布尔逻辑的可满足性问题(SATISFIABLITY problem),简称为SAT,这是历史上第一个被证明的NPC问题。有了第一个NPC问题,一大堆NPC问题就出现了。事实上上文说的哈密顿回路问题就是一个NPC问题。
P=NP ?
现在人们特别想知道P是否等于NP,也就是说是否所有的NP问题都可以在多项式时间内解决。目前P=NP即不能被证明也不能被推翻,事实上我们只要能在多项式时间内解决NPC问题,那么所有的NP问题都可以在多项式时间内解决,也就是P=NP,然而目前已知的NPC问题都没有找到多项式时间的解法。所以现在人们主流认为P不等于NP。





还没有人评论...